Rank SIFT
Rank SIFT algorithm is the revised SIFT (Scale-invariant feature transform) algorithm which uses ranking techniques to improve the performance of the SIFT algorithm. In fact, ranking techniques can be used in key point localization or descriptor generation of the original SIFT algorithm.
Contents |
SIFT With Ranking Techniques
Ranking the Key Point
Ranking techniques can be used to keep certain number of key points which are detected by SIFT detector.[1]
Suppose 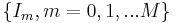 is a training image sequence and
is a training image sequence and  is a key point obtained by SIFT detector. The following equation determines the rank of
is a key point obtained by SIFT detector. The following equation determines the rank of  in the key point set. Larger value of
in the key point set. Larger value of 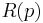 corresponds to the higher rank of
corresponds to the higher rank of  .
.
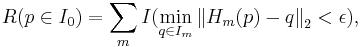
where 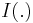 is the indicator function,
is the indicator function, 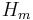 is the homography transformation from
is the homography transformation from 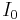 to
to 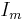 , and
, and  is the threshold.
is the threshold.
Suppose  is the feature descriptor of key point
is the feature descriptor of key point 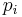 defined above. So
defined above. So  can be labeled with the rank of
can be labeled with the rank of 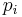 in the feature vector space. Then the vector set
in the feature vector space. Then the vector set 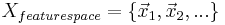 containing labeled elements can be used as a training set for the Ranking SVM[2] problem.
containing labeled elements can be used as a training set for the Ranking SVM[2] problem.
The learning process can be represented as follows:
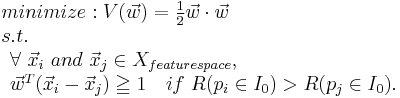
The obtained optimal 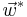 can be used to order the future key points.
can be used to order the future key points.
Ranking the Elements of Descriptor
Ranking techniques also can be used to generate the key point descriptor.[3]
Suppose 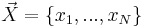 is the feature vector of of a key point and the elements of
is the feature vector of of a key point and the elements of 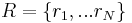 is the corresponding rank of
is the corresponding rank of  in
in  .
. 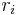 is defined as follows:
is defined as follows:
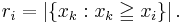
After transforming original feature vector 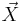 to the ordinal descriptor
to the ordinal descriptor 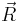 , the difference between two ordinal descriptors can be evaluated in the following two measurements.
, the difference between two ordinal descriptors can be evaluated in the following two measurements.
- The Spearman corelation coefficient
The spearman correlation coefficient also refers to Spearman's rank correlation coefficient. For two ordinal descriptors 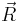 and
and 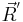 , it can be proved that
, it can be proved that
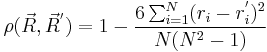
- The Kendall's Tau
The Kedall's Tau also refers to Kendall tau rank correlation coefficient. In the above case, the Kedall's Tau between  and
and 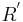 is
is
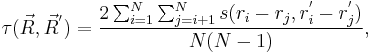
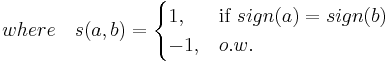
Reference
- ^ Bing Li; Rong Xiao; Zhiwei Li; Rui Cai; Bao-Liang Lu; Lei Zhang; "Rank-SIFT: Learning to rank repeatable local interest points",Computer Vision and Pattern Recognition (CVPR), 2011
- ^ Joachims, T. (2003), "Optimizing Search Engines using Clickthrough Data", Proceedings of the ACM Conference on Knowledge Discovery and Data Mining
- ^ Toews, M.; Wells, W."SIFT-Rank: Ordinal Description for Invariant Feature Correspondence",Computer Vision and Pattern Recognition, 2009.